Technical Guide | Light Cone Module

Cosmological N-body simulations typically adopt a periodic three-dimensional box geometry. This is in contrast to the geometry observed with a telescope, where galaxies are seen distributed along the observer’s light cone. Converting between a box and a light-cone for the purpose of building a mock catalogue is a mechanical yet non-trivial task (Blaizot et al. 2005; Kitzbichler & White 2007; Carlson & White 2010). In TAO, this is taken care of by the light-cone module.

The module can work in two modes. The first is to produce light cones from an entirely unique structure, meaning any galaxy can be selected for the cone from any point in its history at most once. This mode is similar to the method described by Carlson & White (2010). In TAO we concentrate on automated light-cone construction using an analytic solution for the inclination angle calculations. The second mode is for larger light-cones. It is used when it is not possible to fill the light-cone volume without repetitions of the structure. This mode is similar to that described in Blaizot et al. (2005). The TAO algorithm, however, additionally involves random mirroring of the simulation box along the principal axis, increasing the number of pseudo unique volumes by a factor of three. Also, to make the randomized structure even more unique a translation is performed, random shifting along the principal axis. We describe both of these enhancements below. To explain cone construction, we start with some basic concepts and build up to the more sophisticated method used by TAO.

Basics Of Light Cone Creation

To build a basic light cone we place an observer at one of the corners of the simulation box and have them “look out” at the model galaxy distribution. We do this by remapping the Cartesian coordinates of each galaxy into their angular positions in right ascension (RA), declination (Dec) and radial distance (d).

Expanding the Cone Beyond the Box

A problem with the above cone construction becomes apparent when building cones that are deeper in radial extent than the box from which the cone is cut. However, there are a number of ways to deal with this. All of them rely on the fact that most modern simulations are run assuming periodic boundary conditions, meaning that each side of the box connects seamlessly with its opposite side. Below we will assume the box is replicated in all directions, as required to construct such an extended cone. There are now two cases to consider.

Unique Cones

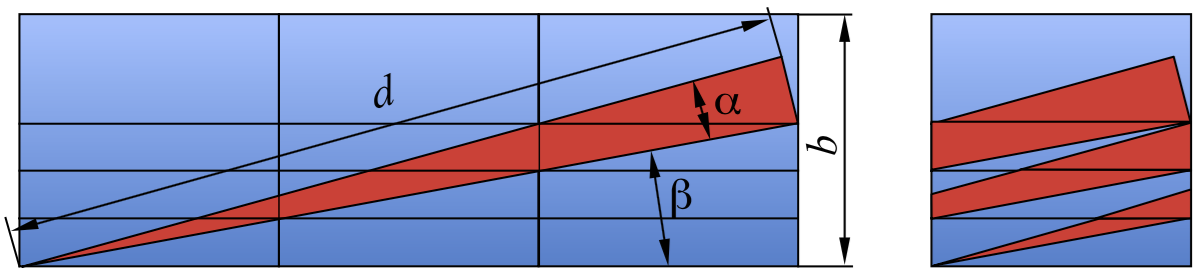
To construct an extended cone we replicate the box in the desired direction and continue the cone construction into this "new" box. To ensure the cone is unique – i.e. any given galaxy in the box along any point in its history is only featured in the cone at most once – we carefully select the viewing angle so that the cone never overlaps with itself as it extends. A similar method is used in Carlson & White (2010).

Within TAO, to optimally select the unique cone viewing angle we need to satisfy the following condition: the light-cone intersection with the furthest and the closest surfaces of the last replicated simulation box must not overlap when both are projected onto a plane of either surface. If this condition is satisfied for the last replicated simulation box, then it will also be satisfied for the rest of the boxes because the light-cone gets narrower closer to the observer, thus making larger gaps between the light-cone path inside the original simulation box.

Random Cones

More typically, however, the volume of the desired cone is larger than the volume of the simulation cube. In this case, one can build a random cone. Although such cones result in the replication of structure, any periodicity can be mitigated somewhat by using randomisation techniques (e.g. Blaizot et al. 2005) which produce a more realistic light-cone with pseudo-unique structure (i.e. repeated but non-periodic). To remove the appearance of periodically repeating structures three randomisation transformations are applied within the TAO light-cone module: random rotation, mirroring, and translation of each repeated simulation cube.

Time Evolution Along the Cone

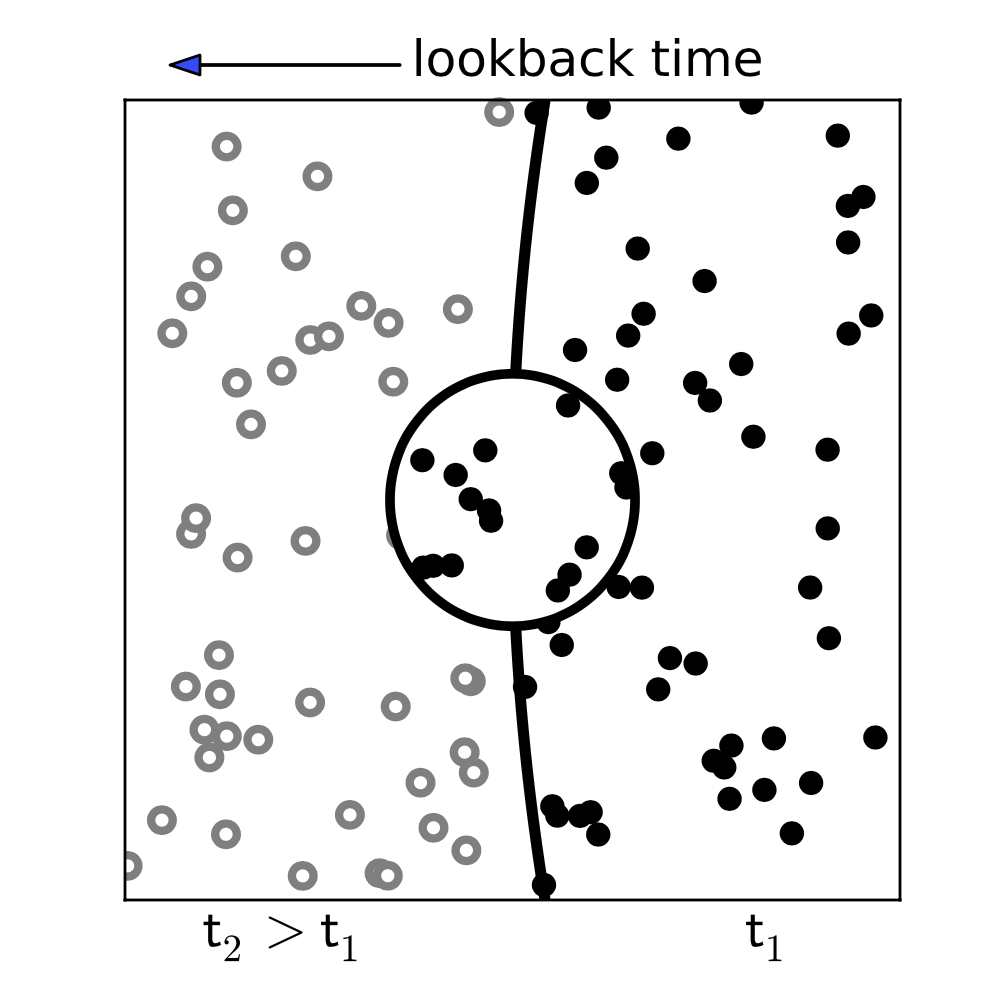
As we progressively move back through the light-cone away from the point of observation we see galaxies from earlier and earlier epochs, due to the time required for the light from each galaxy to cover the distance. Therefore, to construct an accurate cone we need to not only worry about the spatial distribution of the galaxies in it but their evolution as well. Remembering that a galaxy’s radial distance can be directly mapped to a cosmic time, we place each galaxy in the cone as it appeared in the simulation at the age of the Universe corresponding to the distance between the galaxy and the observer. By doing this we also reduce the consequences of structure replication during the cone construction processes. Not only will repeated large-scale structures be seen from different orientations due to the randomisation algorithm described above, but they are likely to be earlier (or later) versions of their duplicates, perhaps appearing differently depending on the growth history of each halo–galaxy system.

There is an additional complication here that is quite subtle yet important: a key part of the light-cone production is to make sure satellite galaxies are always connected to their parent dark matter halo. It often happens that a dark matter halo has its position in the cone very close to the border between different simulation time-steps. If so, satellite galaxies in that halo may inadvertently be split in time across the boundary, and then also be displaced by the randomisation part of the algorithm. In order to provide structural consistency, when building the light-cone, similar to Carlson & White (2010), we group galaxies (centrals and satellites) by their parent halo association as given in the TAO database. Based on the position of the halo centre we then insert these as a unit into the cone, even if the unit spatially crosses the time boundary at any point. This ensures that entire galaxy–halo structures at the same time-step are selected for the cone.